Giải bài 2 trang 62 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho Hình 14, biết ED = EF và EI là tia phân giác của

Đề bài

Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

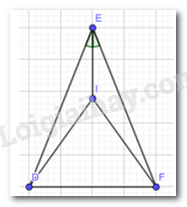
Chứng minh rằng:

a) \(\Delta EID = \Delta EIF\)

b) Tam giác DIF cân

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Ta sử dụng tính chất c-g-c để chứng minh câu a

- Từ câu a ta suy ra ID = FI và chứng minh được tam giác DIF cân

Lời giải chi tiết

a) Xét tam giác EID và tam giác EIF có :

IE chung

ED = EF

\(\widehat {IED} = \widehat {IEF}\)( EI là tia phân giác của \(\widehat {DEF}\))

\( \Rightarrow \Delta EID = \Delta EIF(c - g - c)\)

b) Vì \(\Delta EID = \Delta EIF\) nên ID = IF ( 2 cạnh tương ứng )

Do đó tam giác DIF cân tại I (theo định nghĩa tam giác cân)