Giải bài 41 trang 137 sách bài tập toán 9 - Cánh diều tập 2
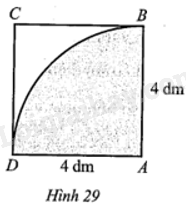
Từ một miếng tôn có dạng hình vuông ABCD cạnh 4 dm, người ta cắt ra một phần tư hình tròn tâm A bán kính AB = 4 dm (như phần được tô màu ở Hình 29) và cuộn lại thành một cái phễu hình nón. Tính chiều cao của cái phễu đó (theo đơn vị decimét và làm tròn kết quả đến hàng phần trăm).
Đề bài
Từ một miếng tôn có dạng hình vuông ABCD cạnh 4 dm, người ta cắt ra một phần tư hình tròn tâm A bán kính AB = 4 dm (như phần được tô màu ở Hình 29) và cuộn lại thành một cái phễu hình nón. Tính chiều cao của cái phễu đó (theo đơn vị decimét và làm tròn kết quả đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
Dựa vào: Chu vi hình tròn \(2\pi R\).
Lời giải chi tiết
Chu vi của một phần tư hình tròn tâm A bán kính AB = 4 dm là:
\(\frac{1}{4}.2\pi .4 = 2\pi \) (dm).
Gọi R là bán kính đường tròn đáy của phễu.
Ta có 2πR = 2π nên R = 1 (dm).
Lại có, đường sinh của phễu là l = 4 dm, suy ra chiều cao của phễu là:
\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{4^2} - {1^2}} = \sqrt {15} \approx 3,87\) (dm)


