Giải bài 6 trang 78 SGK Toán 8 – Cánh diều

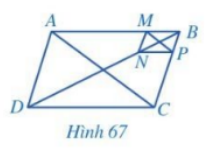
Cho các hình bình hành ABCD và BMNP như ở Hình 67.

Đề bài

Cho các hình bình hành ABCD và BMNP như ở Hình 67. Chứng minh:

a) \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}}\)

b) \( \Delta{MNP} \backsim \Delta{CBA}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Dựa vào định lí Thales suy ra được các tỉ số bằng nhau.

b) Chứng minh MP // AC, suy ra các tỉ số bằng nhau của tam giác PBM và tam giác CBA

BMNP là hình bình hành suy ra các tỉ số bằng nhau của tam giác PBM và tam giác CBA

Từ đó ta suy ra điều phải chứng minh.

Lời giải chi tiết

a) Vì ABCD và BMNP là hình bình hành nên \(MN//BP\) và \(AD//BC \) suy ra \(MN//AD\)

Xét tam giác ABD có \(AD//MN \) nên \(\frac{{BM}}{{BA}} = \frac{{BN}}{{BD}}\) (1) (Định lý Thales)

Tương tự ta chứng minh được \(NP//DC \) nên \(\frac{{BN}}{{BD}} = \frac{{BP}}{{BC}}\) (2)

Từ (1) và (2) ta có \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}}\).

b) Ta có: \(\frac{{BM}}{{BA}} = \frac{{BP}}{{BC}} \) suy ra \(MP//AC\) (Định lý Thales đảo)

Do đó \( \Delta PBM \backsim\Delta CBA\) (c-c-c) (3)

Vì BMNP là hình bình hành nên ta có: \(\frac{{PB}}{{MN}} = \frac{{BM}}{{NP}} = \frac{{MP}}{{PM}} = 1\)

Suy ra \(\Delta PBM \backsim\Delta MNP\) (c-c-c) (4)

Từ (3) và (4) ta có \(\Delta MNP \backsim\Delta CBA\).