Danh Mục
-
Toán 8 tập 1 - Kết nối tri thức với cuộc sống

-
Toán 8 tập 2 - Kết nối tri thức

-
Toán 8 tập 1 - Kết nối tri thức với cuộc sống

-
Toán 8 tập 2 - Kết nối tri thức

Giải bài 9.3 trang 82 SGK Toán 8 tập 2 - Kết nối tri thức
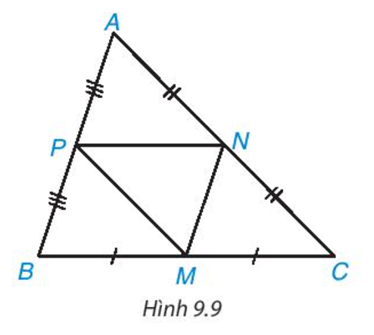
Trong hình 9.9, ABC là tam giác không cân
Đề bài
Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào định lí để chứng minh hai tam giác đồng dạng
Lời giải chi tiết
- Có AP = BP, NA = NC
=> NP // BC (P ∈ AB, N ∈ AC)
=> ΔABC \(\backsim\) ΔAPN
- Có AP = BP, MB = MC
=> MP // AC (P ∈ AB, M ∈ BC)
=> ΔABC \(\backsim\) ΔPBM
- Có NA = NC, MB = MC
=> MN // AB (N ∈ AC,M ∈ BC)
=> ΔABC \(\backsim\) ΔNMC
- Có ΔABC \(\backsim\) ΔAPN và ΔABC \(\backsim\) ΔPBM => ΔAPN \(\backsim\) ΔPBM
- Có ΔABC \(\backsim\) ΔNMC và ΔABC \(\backsim\) ΔPBM => ΔNMC \(\backsim\) ΔPBM
- Có ΔAPN \(\backsim\) ΔPBM và ΔNMC \(\backsim\) ΔPBM => ΔAPN \(\backsim\) ΔNMC
🎉 Khuyến Mãi Đặc Biệt: Tải App BeautZone Ngay!

BeautZone - Ứng dụng làm đẹp, Ứng dụng của người Việt
📱 Tải app ngay để nhận giảm 50% sản phẩm PRO!
✅ Khám phá skincare, makeup, tóc giả, phụ kiện từ các thương hiệu yêu thích.
✨ Làm đẹp dễ dàng, giao hàng nhanh chóng tận tay bạn.

