Giải bài tập 6 trang 87 SGK Toán 9 tập 1 - Cánh diều
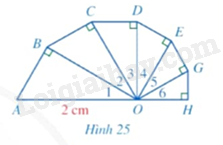
Tính độ dài đường gấp khúc (ABCDEGH), biết các tam giác (OAB,OBC,OCD,ODE,OEG,OGH) là các tam giác vuông tại các đỉnh lần lượt là (B,C,D,E,G,H); các góc ({O_1},{O_2},{O_3},{O_4},{O_5},{O_6}) đều bằng (30^circ ) và (OA = 2cm) (Hình 25).
Đề bài
Tính độ dài đường gấp khúc \(ABCDEGH\), biết các tam giác \(OAB,OBC,OCD,ODE,OEG,OGH\) là các tam giác vuông tại các đỉnh lần lượt là \(B,C,D,E,G,H\); các góc \({O_1},{O_2},{O_3},{O_4},{O_5},{O_6}\) đều bằng \(30^\circ \) và \(OA = 2cm\) (Hình 25).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải chi tiết
Xét tam giác \(ABO\) vuông tại \(B\), ta có:
+) \(AB = AO.\sin 30^\circ = 2.\sin 30^\circ = 1\left( {cm} \right)\).
+) \(BO = AO.\cos 30^\circ = 2.\cos 30^\circ = \sqrt 3 \left( {cm} \right)\).
Xét tam giác \(BOC\) vuông tại \(C\), ta có:
+) \(BC = BO.\sin 30^\circ = \sqrt 3 .\sin 30^\circ = \frac{{\sqrt 3 }}{2}\left( {cm} \right)\).
+) \(CO = BO.\cos 30^\circ = \sqrt 3 .\cos 30^\circ = \frac{3}{2}\left( {cm} \right)\).
Xét tam giác \(COD\) vuông tại \(D\), ta có:
+) \(CD = CO.\sin 30^\circ = \frac{3}{2}.\sin 30^\circ = \frac{3}{4}\left( {cm} \right)\).
+) \(DO = CO.\cos 30^\circ = \frac{3}{2}.\cos 30^\circ = \frac{{3\sqrt 3 }}{4}\left( {cm} \right)\).
Xét tam giác \(DOE\) vuông tại \(E\), ta có:
+) \(DE = DO.\sin 30^\circ = \frac{{3\sqrt 3 }}{4}.\frac{1}{2} = \frac{{3\sqrt 3 }}{8}\left( {cm} \right)\).
+) \(EO = DO.\cos 30^\circ = \frac{{3\sqrt 3 }}{4}.\frac{{\sqrt 3 }}{2} = \frac{9}{8}\left( {cm} \right)\).
Xét tam giác \(EOG\) vuông tại \(G\), ta có:
+) \(EG = EO.\sin 30^\circ = \frac{9}{8}.\frac{1}{2} = \frac{9}{{16}}\left( {cm} \right)\).
+) \(GO = EO.\cos 30^\circ = \frac{9}{8}.\frac{{\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{{16}}\left( {cm} \right)\).
Xét tam giác \(GOH\) vuông tại \(H\), ta có:
\(GH = GO.\sin 30^\circ = \frac{{9\sqrt 3 }}{{16}}.\frac{1}{2} = \frac{{9\sqrt 3 }}{{32}}\left( {cm} \right)\).
Vậy độ dài đường gấp khúc \(ABCDEGH\) là:
\(ABCDEGH = 1 + \frac{{\sqrt 3 }}{2} + \frac{3}{4} + \frac{{3\sqrt 3 }}{8} + \frac{9}{{16}} + \frac{{9\sqrt 3 }}{{32}} = \frac{{37\left( {2 + \sqrt 3 } \right)}}{{32}} \approx 4,3 \left( {cm} \right)\).


