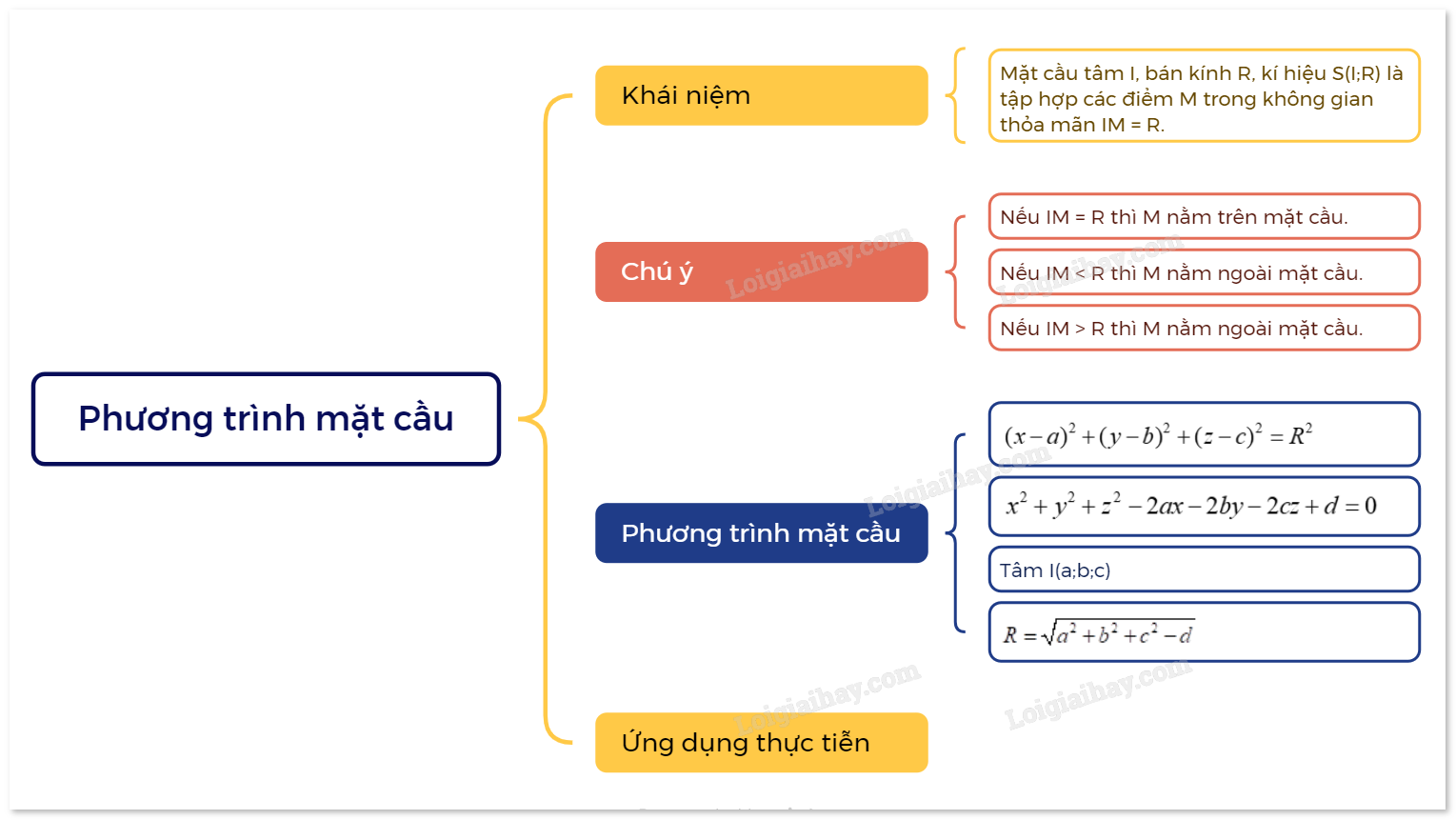
Lý thuyết Phương trình mặt cầu Toán 12 Chân trời sáng tạo
1. Phương trình mặt cầu trong không gian Khái niệm mặt cầu Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.
1. Phương trình mặt cầu trong không gian
Khái niệm mặt cầu
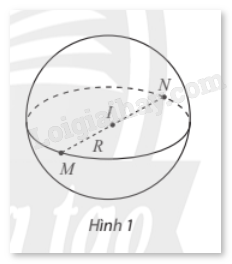
Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.
Chú ý: Cho mặt cầu S(I;R).
Nếu IM = R thì M nằm trên mặt cầu.
Nếu IM < R thì M nằm ngoài mặt cầu.
Nếu IM > R thì M nằm ngoài mặt cầu.
Phương trình mặt cầu
|
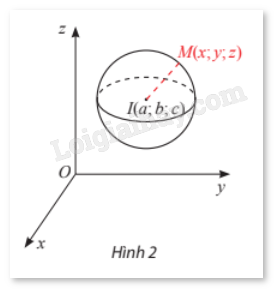
Trong không gian Oxyz, mặt cầu (S) tâm I(a;b;c) bán kính R có phương trình \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\) |
Nhận xét: Phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \({a^2} + {b^2} + {c^2} - d > 0\) là phương trình của mặt cầu tâm I(a;b;c) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Ví dụ 1: Viết phương trình mặt cầu (S):
a) Có tâm I(1;2;3), bán kính R = 5.
b) Có đường kính AB với A(1;3;7) và B(3;5;1).
c) Có tâm A(1;0;2) và đi qua điểm B(2;4;1).
Giải:
a) Mặt cầu (S) có phương trình \({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 25\).
b) Mặt cầu (S) có đường kính AB nên có tâm J(2;4;4) là trung điểm AB và bán kính R = JA = \(\sqrt {11} \).
Vậy (S) có phương trình \({(x - 2)^2} + {(y - 4)^2} + {(z - 4)^2} = 11\).
c) Mặt cầu (S) có tâm A(1;0;-2) và đi qua điểm B(2;4;1) nên có bán kính R = AB = \(\sqrt {26} \).
Vậy (S) có phương trình \({(x - 1)^2} + {y^2} + {(z + 2)^2} = 26\).
Ví dụ 2: Xác định tâm và bán kính mặt cầu có phương trình:
a) (S): \({(x - 3)^2} + {(y - 7)^2} + {(z + 1)^2} = 81\).
b) (S’): \({x^2} + {y^2} + {z^2} = 4\).
Giải:
a) Mặt cầu (S) có tâm I(3;7;-1) và bán kính R = \(\sqrt {81} \) = 9.
b) Mặt cầu (S’) có tâm O(0;0;0) và bán kính R’ = \(\sqrt 4 \) = 2.
Ví dụ 3: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\).
b) \({x^2} + {y^2} + {z^2} + x + y - 6z + 33 = 0\).
Giải:
a) Phương trình \({x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - 4;b = 3;c = - 1;d = - 10\).
Ta có \({a^2} + {b^2} + {c^2} - d = 16 + 9 + 1 + 10 = 36 > 0\).
Suy ra phương trình đã cho là phương trình mặt cầu tâm I(-4;3;-1), bán kính R = 6.
b) Phương trình \({x^2} + {y^2} + {z^2} + x + y - 6z + 33 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - \frac{1}{2};b = - \frac{1}{2};c = 3;d = 33\).
Ta có \({a^2} + {b^2} + {c^2} - d = \frac{1}{4} + \frac{1}{4} + 9 - 33 = - \frac{{47}}{2} < 0\).
Suy ra phương trình đã cho không phải phương trình mặt cầu.
2. Vận dụng của phương trình mặt cầu
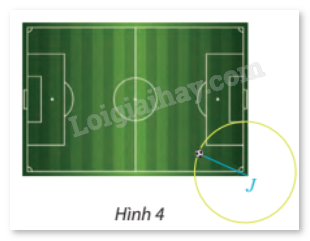
Ví dụ: Công nghệ hỗ trợ trọng tài VAR (Video Assisstant Referee) thiết lập một hệ tọa độ Oxyz để theo dõi vị trí của quả bóng M. Cho biết M đang nằm trên mặt sân có phương trình z = 0, đồng thời thuộc mặt cầu (S): \({(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109\) (đơn vị độ dài tính theo mét).
a) Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
b) Tìm tọa độ hình chiếu vuông góc J của tâm I trên mặt sân.
c) Tính khoảng cách từ vị trí M của quả bóng đến điểm J.
Giải:
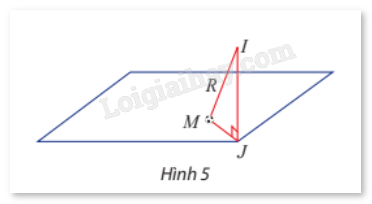
Mặt cầu (S) có phương trình \({(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109\) nên có tâm I(32;50;0) và bán kính \(R = \sqrt {109} \).
b) Trong không gian Oxyz, mặt sân có phương trình z = 0 trùng với mặt phẳng tọa độ (Oxy), suy ra hình chiếu vuông góc của điểm I(32;50;10) xuống mặt sân có tọa độ J(32;50;0).
c) Trong tam giác vuông IJM, ta có IJ = 10, IM = R, suy ra
\(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {109 - 100} = 3\).
Vậy khoảng cách từ vị trí M của quả bóng đến điểm J là 3m.