Lý thuyết Vị trí tương đối của đường thẳng và đường tròn Toán 9 Cánh diều

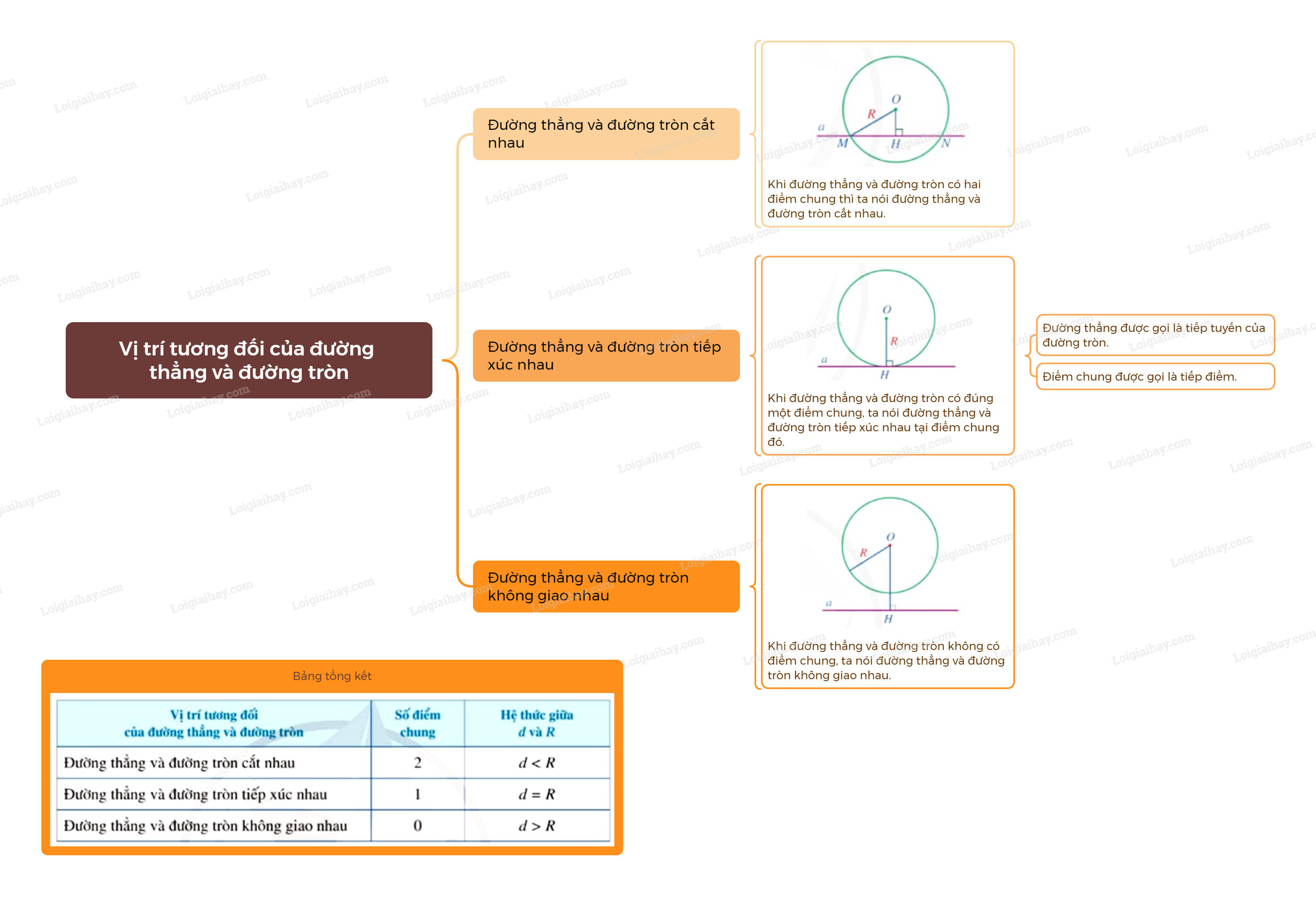
1. Đường thẳng và đường tròn cắt nhau Khi đường thẳng và đường tròn có hai điểm chung thì ta nói đường thẳng và đường tròn cắt nhau. Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.

1. Đường thẳng và đường tròn cắt nhau

Khi đường thẳng và đường tròn có hai điểm chung thì ta nói đường thẳng và đường tròn cắt nhau.

Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.

Nhận xét: Đường thẳng a cắt đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a nhỏ hơn R và ngược lại.

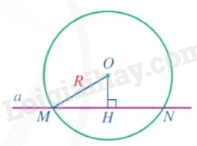
2. Đường thẳng và đường tròn tiếp xúc nhau

Khi đường thẳng và đường tròn có đúng một điểm chung, ta nói đường thẳng và đường tròn tiếp xúc nhau tại điểm chung đó.

Nếu đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn, điểm chung được gọi là tiếp điểm.

Nhận xét: Đường thẳng a tiếp xúc với đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a bằng R và ngược lại.

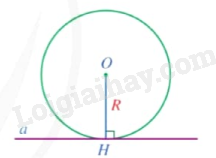
3. Đường thẳng và đường tròn không giao nhau

Khi đường thẳng và đường tròn không có điểm chung, ta nói đường thẳng và đường tròn không giao nhau.

Nhận xét: Đường thẳng a và đường tròn (O;R) không giao nhau khi khoảng cách từ tâm O đến đường thẳng a lớn hơn R và ngược lại.

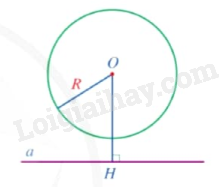
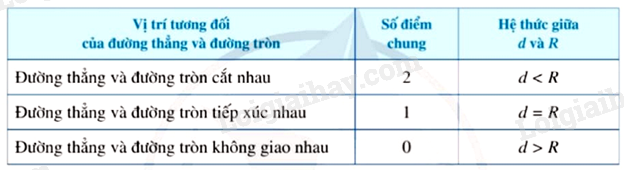
Nhận xét: Ta có thể nhận biết vị trí tương đối của đường thẳng a và đường tròn (O;R) thông qua hệ thức giữa khoảng cách d từ tâm O đến đường thẳng a và bán kính R được tóm tắt trong bảng sau:

Danh Mục

Lý thuyết Vị trí tương đối của đường thẳng và đường tròn Toán 9 Cánh diều

1. Đường thẳng và đường tròn cắt nhau Khi đường thẳng và đường tròn có hai điểm chung thì ta nói đường thẳng và đường tròn cắt nhau. Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.